Object Orientation, Principal Component Analysis & OpenCV

A friend of mine recently asked me how to detect the orientation of various 2D objects in an image. For example consider the objects in the images below, how would you find the orientation of each object?

My first idea was to come up with some ad hoc geometrical analysis for each shape, but then suddenly I realised that Principal Component Analysis (PCA) could give a generic answer to the problem. I got interested in the idea, so I sat down and I wrote a program in C++ that performs PCA analysis using OpenCV. The result was a short program which worked so well, that I decided to make a small tutorial on PCA & OpenCV based on it.

What is PCA?

PCA is a mathematical tool that extracts the most important features of a dataset. For a detailed and mathematical explanation check Wikipedia or any textbook on statistics. I will try to give you a more intuitive understanding of what PCA does.

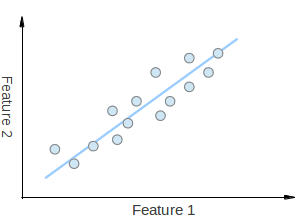
Suppose you had a set of 2D points as shown in the figure above, where each dimension corresponds to a feature you are interested in. Some could argue that the points are random, but there is a linear pattern (indicated by the blue line) which is hard to dismiss. It is possible to approximate the set of points to a single line i.e. reduce the dimensionality of the points from 2D to 1D. Dimensionality reduction is a key technique in artificial intelligence and data mining. You could also see that the points vary the most along the blue line, more than they vary along the Feature 1 or Feature 2 axes. This means that if you know the position of a point along the blue line you have more information about the point than if you only knew where it was on Feature 1 axis or Feature 2 axis.

So PCA is a mathematical tool which allows us to find the direction along which our data varies the most. In fact, the result of running PCA on the set of points in the diagram consist of 2 vectors called eigenvectors which are the principal components of the data set.

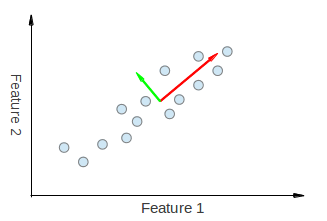The size of each eigenvector is encoded in the corresponding eigenvalue and indicates how much the data vary along the principal component. The beginning of the eigenvectors is the centre of all points in the data set. Applying PCA to N-dimensional data set yields N N-dimensional eigenvectors, N eigenvalues and 1 N-dimensional centre point. Enough theory, let’s see how we can put these ideas into code.

Implementation

If you understand the maths behind the PCA it would be a good idea to spend several hours and implement it on your own just for the sake understanding it even better. If you just want to use PCA as a black box (input data -> SOME MAGIC -> principal components) then you should find a library which offers that functionality. Since the problem is related to image processing I used OpenCV and as it turns out OpenCV supports PCA. So lets see step by step how  calculate the orientation of each object in the images above.

First, read the image and convert it to greyscale.

Mat bw, img = imread("test_image.jpg");
cvtColor(img, bw, COLOR_BGR2GRAY);

Then process the greyscale image and find the objects of interest.

// Apply thresholding;
threshold(bw, bw, 150, 255, CV_THRESH_BINARY);

// Find all the contours in the thresholded image
vector<vector<Point> > contours;
vector<Vec4i> hierarchy;
findContours(bw, contours, hierarchy, CV_RETR_LIST, CV_CHAIN_APPROX_NONE);

Finally, filter out contours with inappropriate size and find the orientation of the remaining ones.

for (size_t i = 0; i < contours.size(); ++i)
{
    // Calculate the area of each contour
    double area = contourArea(contours[i]);
    // Ignore contours that are too small or too large
    if (area < 1e2 || 1e5 < area) continue;

    // Draw each contour only for visualisation purposes
    drawContours(img, contours, i, CV_RGB(255, 0, 0), 2, 8, hierarchy, 0);
    // Find the orientation of each shape
    getOrientation(contours[i], img);
}

All of the PCA “magic” happens in the getOrientation() function which is shown below:

double getOrientation(vector<Point> &pts, Mat &img)
{
    //Construct a buffer used by the pca analysis
    Mat data_pts = Mat(pts.size(), 2, CV_64FC1);
    for (int i = 0; i < data_pts.rows; ++i)
    {
        data_pts.at<double>(i, 0) = pts[i].x;
        data_pts.at<double>(i, 1) = pts[i].y;
    }

    //Perform PCA analysis
    PCA pca_analysis(data_pts, Mat(), CV_PCA_DATA_AS_ROW);

    //Store the position of the object
    Point pos = Point(pca_analysis.mean.at<double>(0, 0),
                      pca_analysis.mean.at<double>(0, 1));

    //Store the eigenvalues and eigenvectors
    vector<Point2d> eigen_vecs(2);
    vector<double> eigen_val(2);
    for (int i = 0; i < 2; ++i)
    {
        eigen_vecs[i] = Point2d(pca_analysis.eigenvectors.at<double>(i, 0),
                                pca_analysis.eigenvectors.at<double>(i, 1));

        eigen_val[i] = pca_analysis.eigenvalues.at<double>(0, i);
    }

    // Draw the principal components
    circle(img, pos, 3, CV_RGB(255, 0, 255), 2);
    line(img, pos, pos + 0.02 * Point(eigen_vecs[0].x * eigen_val[0], eigen_vecs[0].y * eigen_val[0]) , CV_RGB(255, 255, 0));
    line(img, pos, pos + 0.02 * Point(eigen_vecs[1].x * eigen_val[1], eigen_vecs[1].y * eigen_val[1]) , CV_RGB(0, 255, 255));

    return atan2(eigen_vecs[0].y, eigen_vecs[0].x);
}

The PCA API of C++ is somewhat awkward because we cannot pass an array of 2D points, but we have to arrange them in a matrix with size n x 2 where n is the number of data points we have (lines 4-9). We construct a PCA object in line 12 which automatically runs PCA on the input data given as the first argument (data_pts). The second argument is the centre of the data set, but since we do not know it we pass an empty matrix Mat(), meaning that it will be estimated. The final argument indicates how the data is supplied – in our case it is CV_PCA_DATA_AS_ROW because each point is a row in the input matrix (data_pts). The calculated mean is stored in the pos variable (lines 14-16) and the eigenvectors and eigenvalues are stored in std::vector’s (lines 18-27). The operations between line 14 and 27 are not necessary, but drastically increase the readability of the code. The principal components are drawn in lines 30-32, where each eigenvector is multiplied by its eigenvalue and translated to the mean position. There is a 0.02 scaling coefficient which is there only to make sure that the vectors fit in the image and do not have length of 10000 pixels. Eventually, the angle of the first eigenvector (the strongest one i.e. with largest eigenvalue) is calculated and returned. You can download the project including source code, Makefile and images from here.

Results

So these are the results after running the PCA on the images. As you can see the principal components do a very neat job at describing the orientation of an object. You should bare in mind, though, that the resulting axis is the one with greatest variance of the data points, which does not necessary reflect a key structural feature of the shape as it can be seen from the shape formed by two rectangles. Despite that, it is a valid description of orientation which could be obtained for any shape.